The aim of this paragraph is to introduce the curious reader to the construction of FIRENET and the underlying theory. See the blog post.

As we mentioned before, a model is unstable if there exist a small (in norm) perturbation which, if applied to the input, changes the output of the model significantly. Analyzing the instability from a theoretical point of view, we can determine a necessary condition for a model to be stable, namely kernel awareness. Intuitively, a reconstruction method lacks kernel awareness if it over performs on the reconstruction of two vectors whose difference of the measurements is small in norm. In other words, the lack of kernel awareness can be seen as the overfitting of a model for the resolution of an inverse problem, and it is made more likely by the typical deep learning training procedure.

Compressed Sensing theory can be exploited to find some assumptions on the sub-sampling operator A that ensure kernel awareness of the reconstruction model. Compressed Sensing is a research field that aims at the reconstruction of a signal from incomplete linear information assuming that the signal has a sparsity structure. Furthermore, in order to avoid a training procedure, the neural network was constructed by unrolling the Primal-Dual optimization algorithm described in [1] applied to the optimizaion problem.

We present some results, mathematically confirming the visual impressions. The quantitative comparison between FIRENET and the bicubic interpolation is displayed through two metrics: root mean squared error (RMSE) and peak signal-to-noise ratio (PSNR), given by
PSNR(x,z) = 20 \log_{10} \frac{max(x,z)}{RMSE(x,z)}.
where x is the ground truth, z is the restored SR image and max(x,z) defines the maximum pixel value of x and z. Moreover, to measure the noise magnitude relative to the image, we use the Noise Over Measurement (NOM), which is simply the norm of the error over the norm of the input y.

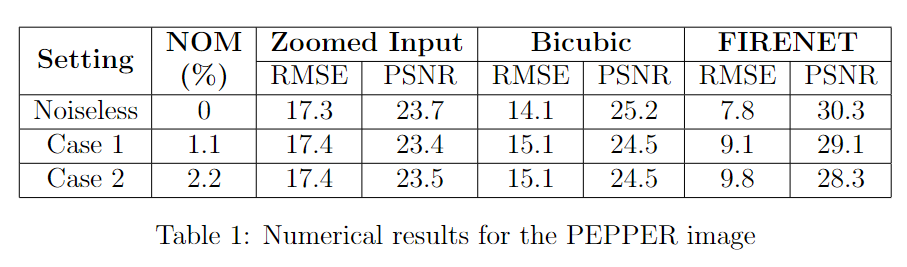
Lastly, we repeated the reconstruction using two different high-resolution images, in order to show that the performance obtained on the PEPPER image are not restricted to this single case. The visual analysis is displayed in the following image.